Matematika a zenében
„matematika legalább annyira művészet, mint tudomány”

„A zene, az hangzó matematika.”
/Kodály Zoltán/

A világon mindenhol “elől van a matematika és a nyelvek, aztán a humán tárgyak. A művészetek között is hierarchia van: a zene mindig előrébb van, mint a dráma vagy tánc.” mondta Sir Ken Robinson, egy 2006-os TED konferencián. A püthagoreusok a matematikai igazságok megnyilvánulásának tekintették a zenét; ők fedezték fel bizonyos matematikai arányok és zenei hangközök egybeesését. Matematikailag kiszámolható, hogy a kromatikus skála 12 hangjának lehetséges kombinációija több mint egybillió (pontosan: egybillió-háromszázkétmillió-hatvanegyezer-háromszáznegyvennégy). És ez a csillagászati szám csak az egy-hangból álló dallam variálhatóságára vonatkozik. Ha a dallamok és harmóniák egymással kombinálható lehetőségeit a ritmikai variációk változatosságával is kiegészítjük, akkor megállapítható, hogy a zene birodalma végtelen.

A matematika és zene kapcsolatát rendkívül izgalmas vizsgálni és érdekes kérdéseket is vet fel. Hogyan lehetséges a főként érzelmek kifejezésére használt zene és a természetet leíró matematika között bármiféle összeköttetés? Mindkét tudomány, vagy művészet sajátos nyelvezettel rendelkezik, mindkettő külön világ, mégis már a történelem során számos neves embert foglalkoztatott a kérdés. Nagy tudósok, polihisztorok életében mindig is fontos szerepet játszott a zene, talán innen is eredeztethető a két terület közötti összefüggések vizsgálata.

A zenei struktúrában a legszembetűnőbb a matematika. Több zeneszerzőt érdekelt az aranymetszés, többek között Bartókot. Később logikai „tervek” alapján szerezték a műveket. Ám a zenében fellelhető legradikálisabb példa egy matematikusnál, Xenakisnál jelentkezik, aki egy parabolát, és más, egyéb izgalmas függvényt próbált megzenésíteni.

Azt gondolná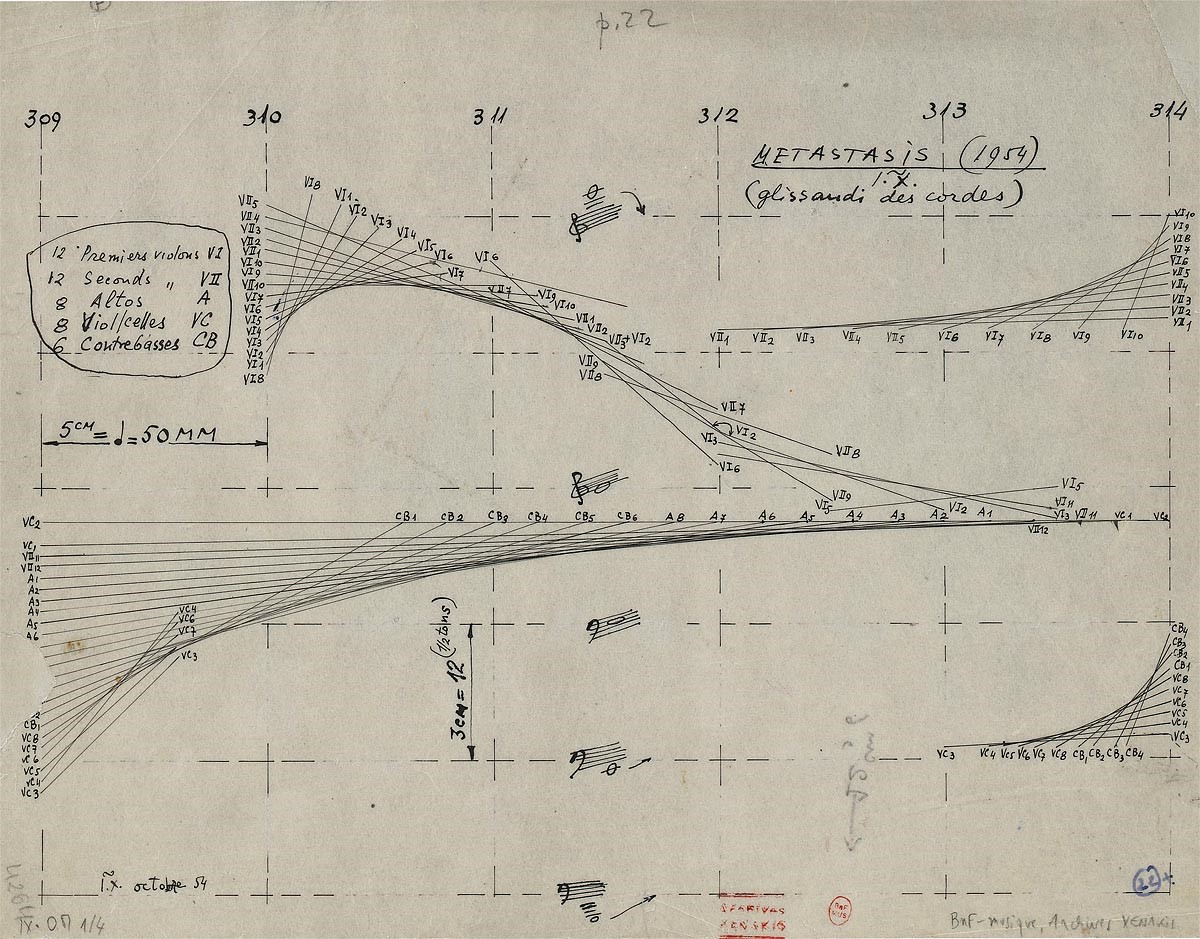 az ember, hogy a fizika mégis közelebb áll a zenéhez, mint a matematika. Sokan talán azt gondolják, hogy a zene, mint művészet, egyfajta logikátlansággal teli és csupán megérzéseken alapuló tudomány, míg a matematika egy nagyon is racionális, jól felépített, logikus és ellentmondásmentes következtet rendszer. Talán azt mondhatná a laikus, hogy a két területben semmi hasonlóság nincsen. Ez a helyzet például a hang magasságánál és a felhangoknál nyilvánul meg.

Mi a hang? A hang tulajdonképpen rezgés. A rezgés és hang fogalmát néha könnyű, és néha nehezebb elválasztani egymástól. Ha megszólaltatunk egy hangvillát, a villa elkezd rezegni, a körülötte lévő levegő átveszi a rezgését, ami eljut a fülbe, átviszi a rezgést a dobhártya, és végül ez a rezgés alakul át hangélménnyé az agyban. A hangvilla rezgését magunk is megjeleníthetjük, ha a hangvilla végére egy tűt erősítünk, majd rezgésbe hozzuk egy viaszos, vagy faszenes lapot húzunk el alatta. Szabályos hullámvonalakat fogunk kapni, amit a matematikában szinuszgörbeként ismerünk.

De először vessünk pillantást egy kottára. A legelső, amit megpillantunk egy zenei kulcs. Violinkulcs, vagy basszuskulcs. Ha megnézzük ezeket a kulcsokat, akkor mindkettőben megtalálhatunk egy csigavonalra emlékeztető alakzatot. Aki tapasztaltabb, az láthatja, hogy ez nem más, mint egy aranymetszés.

„A tudomány olyan, mint egy Stradivari, a legjobb hegedű
a világon. De a megszólaltatásához jól kell tudni játszani,
és ismerni kell a zenét. Máskülönben nem szól szebben,
mint bármely más hegedű”.
/Pjotr Kapica/

A hangnemet szorosan követi az ütemmutató. Ez a matematikából jól ismert tört számmal jelölendő. A nevező jelöli a hang hosszát, a számláló pedig megmutatja, hogy egy ütem mennyi ritmust tartalmaz. Mint a számtanban, itt is lehetséges a páros és páratlan ütemmutató.

Hogy egy egész ütembe beleférjenek a hangok, felosztjuk azokat. A legtöbb esetben felezzük a hangokat. A 4/4-et kitöltő hangot egész hangnak nevezzük. Ha ezt kettéosztjuk két feletkapunk. Ezt tovább osztva negyedeket, nyolcadokat, tizenhatodokat, vagy akár harminckettedeket kaphatunk. Ebből a hangkészletből 3/4, 3/8, 3/16 (vagy 5/4, 7/4…) hosszúságú hangokat is összeállíthatunk. A 3/4-es hanghoz egy fél és egy negyed összekapcsolásával juthatunk, vagyis két különböző értékű hangot összeadunk. A két terület közötti hasonlóság itt is megmutatkozik, hiszen ugyanúgy összeadhatók, oszthatók a hangok is, mint a számok (jelen esetben a hangok időtartamára értendő).

Fontos még megemlíteni a hangmagasságot. Ez két hang közötti távolságot jelent, vagyis milyen mélynek, illetve magasnak halljuk a hangot. A „görög ókorban” kezdetben volt a zene, ami „szülte” a számelméletet, majd e kettő vált a pitagoreusok filozófiájának, a harmóniatannak az alapjává. Feltették a kérdést: mi a feltétele annak, hogy két egymásutánban hallatott hang a fül számára kellemes legyen, a harmónia érzetét keltse? Ezeket a távolságokat különböző skálákon osztották be, attól függően mikor melyik skálát használták. Ahhoz, hogy ez létrejöhessen, első lépésként egy hangsort kellett megalkotni. a zenei hangkészlet „tagjait” az ABC nagybetűivel jelöljük. Mint ismeretes, a dúr hangsor jellegzetessége a 2 egész, 1 fél; 3 egész, 1 fél szerkezet. Kialakulására állítólag az jellemző, hogy a CDEF (tehát a nagyszekund-nagyszekund-kisszekund szerkezet) hangsor ismétlődik meg egy kvinttel feljebb (GAHC).

A törzshangokon kívül származtatott zenei hangok is vannak, ezeket a törzshangokmódosításával kapjuk. Ehhez bevezetjük a módosítójel fogalmát.

Püthagorasz tanítványaival különböző hosszúságú kifeszített húrokat megpendítve kísérletezett, és arra a felismerésre jutott, hogy a konszonáns hangzatok hangzásakor a húrhosszak aránya rendre: 2 : 1; 3 : 2; 4 : 3.

Összesen két alaphangközt, a kvintet és az oktávot használva felépítettek egy skálát, melyet róluk püthagoraszi skálának neveztek el. Észrevették továbbá, hogy két hangköz kivonásával, egy harmadik hangköz nyerhető, méghozzá a kvart:

oktáv – kvint = kvart

Két hangköz összeadásának, illetve kivonásának megfeleltethet a hangközöket jellemző húrarányszámok szorzata, illetve hányadosa, jelen példában:

(2 : 1) : (3 : 2) = (4 : 3)

„Ha a dallamok és harmóniák egymással kombinálható
lehetőségeit a ritmikai variációk változatosságával
is kiegészítjük, akkor megállapítható,
hogy a zene birodalma végtelen.”

A történelem során nem csak a görögök foglalkoztak a zene és a matematika kapcsolatával, és akik ezzel foglalkoztak sem mind matematikus volt. Akadtak köztük vegyészek, fizikusok is: Euler, Gauss, Bólyai Farkas és János, Farkas Gyula, Fejér Lipót, Einstein, Kepler, Newton, Heimholtz, Planck és a sor még hosszasan folytatható és napjainkban is gyarapítható. Ezen a határterületen tett vizsgálódások, kutatások, megállapítások mindkét tudományterület fejlődését szolgálja.

Az írásban csak egy nagyon kis részletébe tekintettünk, miként tud e két művészet kapcsolódni egymáshoz. Ezen kívül más megközelítések, elméletek, magyarázatok is léteznek.

„A zene legalább annyira tudomány, mint művészet”

Források

https://prezi.com/iinoqd810iue/zene-es-matematika-kapcsolata/

http://www.zenci.hu/szocikk/matematika

http://zeneszerzo.blog.hu/2010/11/23/matematika_a_zeneben_zene_a_matematikaban

http://www.termeszetvilaga.hu/tv2001/tv0110/bagi.html

http://members.iif.hu/visontay/ponticulus/rovatok/hidverok/mat_fiz_kem_zene.html

http://hirmagazin.sulinet.hu/hu/pedagogia/zene-es-matematika

Kanizsai Rita: Zenei fogalmak és rendszerek a matematika nyelvén, Letöltve:2015.06.07.